基于Numpy的线性代数运算
本文共 4633 字,大约阅读时间需要 15 分钟。
标题中的英文首字母大写比较规范,但在python实际使用中均为小写。
1.Numpy中的matrix
1.1 创建matrix对象
numpy.matrix方法的参数可以为ndarray对象
numpy.matrix方法的参数也可以为字符串str,示例如下:import numpy as npm = np.matrix("1 2 3;4 5 6; 7 8 9")print(m,type(m)) 上面一段代码的运行结果如下:
[[1 2 3]
[4 5 6] [7 8 9]] <class 'numpy.matrixlib.defmatrix.matrix'>
1.2 bmat函数
很神奇的用法, 可以用字符串和已定义的矩阵创建新矩阵。
import numpy as npa = np.eye(2)print("a :\n",a)b = a * 2print("b :\n",b)c = np.bmat("a b;b a")print("c :\n",c) 上面一段代码的运行结果如下:
a :
[[1. 0.] [0. 1.]] b : [[2. 0.] [0. 2.]] c : [[1. 0. 2. 0.] [0. 1. 0. 2.] [2. 0. 1. 0.] [0. 2. 0. 1.]]
2.算术运算
2.1 ndarray对象的除法运算
5种除法运算方式:
1.divide函数:做除法,返回除法的浮点数结果 2.true_divide函数:返回除法的浮点数结果 3.floor_divide函数:做除法,进行向下取整并返回整数 4.使用/运算符:相当于调用divide函数 5.使用//运算符:相当于调用floor_divide函数 示例代码如下:import numpy as np a = np.array([2,6,5])b = np.array([1,2,3])print("divide function result:")print(np.divide(a,b))print(np.divide(b,a))print("true_divide function result:")print(np.true_divide(a,b))print(np.true_divide(b,a))print("floor_divide function result:")print(np.floor_divide(a,b))print(np.floor_divide(b,a)) 上面一段代码的运行结果如下:
divide function result:
[ 2. 3. 1.66666667] [ 0.5 0.33333333 0.6 ] true_divide function result: [ 2. 3. 1.66666667] [ 0.5 0.33333333 0.6 ] floor_divide function result: [2 3 1] [0 0 0]
2.2 ndarray对象的模运算
4种模运算方式:
1.remainder函数:逐个返回两个数组中元素相除后的余数 2.mod函数与remainder函数,两者功能完全一致 3.%操作符是remainder函数的简写 4.fmod函数所得余数的正负由被除数决定,与除数的正负无关 示例代码如下:import numpy as npa = np.arange(-5,5)print("remainder function result:")print(np.remainder(a,3))print("mod function result:")print(np.mod(a,3))print("% operator result:")print(a % 3)print("fmod function result:")print(np.fmod(a,3)) 上面一段代码的运行结果如下:
remainder function result:
[1 2 0 1 2 0 1 2 0 1] mod function result: [1 2 0 1 2 0 1 2 0 1] % operator result: [1 2 0 1 2 0 1 2 0 1] fmod function result: [-2 -1 0 -2 -1 0 1 2 0 1]
3.通用函数
概念:通用函数是一种对ndarray中的数据执行元素级运算的元素。你可以将其看做其他函数(接受一个或者多个标量,并产生一个或多过标量值)的矢量化包装器。通用函数的输入是一组的标量,输入也是一组标量,它们通常可以对应于基本数学运算,如加、减、乘、除。
ufunc有两个类别: 1.一元(unary)ufunc,它们接受一个数组。返回一个结果数组,当然也能返回两个数组,但是这种的不是很常见; 2.二元(binary)ufunc,它们接受两个数组, 并返回一个结果数组。一元(unary)ufunc

image.png
二元(binary)ufunc

image.png
Numpy已有的通用函数具备的方法
4种方法:
1 np.add.accumulate返回对矩阵求和结果,和np.sum效果相同,返回值数据类型为整数int 2 np.add.reduce返回求和运算的中间结果,返回值数据类型为numpy.ndarray 3 np.add.reduceat返回值数据类型为numpy.ndarray 返回ndarray对象的第1个元素是0,5返回索引0-4对应值的求和结果 返回ndarray对象的第2个元素是5,2返回索引5对应值 返回ndarray对象的第3个元素是2,7返回索引2-6对应值的求和结果,即3+4+5+6+7=25 返回ndarray对象的第4个元素是7-end返回索引7-9对应值的求和结果,即8+9+10=27 4 np.add.outer返回值数据类型为numpy.ndarray 返回ndarray对象的第1个元素是a所有元素+1的结果 返回ndarray对象的第2个元素是a所有元素+2的结果 返回ndarray对象的第3个元素是a所有元素+3的结果import numpy as npa = np.arange(1,11)print("add.reduce result:")print(np.add.reduce(a))print("add.accumulate result:")print(np.add.accumulate(a))print("add.reduceat result:")print(np.add.reduceat(a,[0,5,2,7]))print("add.outer result:")print(np.add.outer(np.arange(1,4),a)) 上面一段代码的运行结果如下:
add.reduce result:
55 add.accumulate result: [ 1 3 6 10 15 21 28 36 45 55] add.reduceat result: [15 6 25 27] add.outer result: [[ 2 3 4 5 6 7 8 9 10 11] [ 3 4 5 6 7 8 9 10 11 12] [ 4 5 6 7 8 9 10 11 12 13]]
4.线性代数应用
numpy.linalg模块包含线性代数的函数。使用这个模块,可以用来:
1.计算逆矩阵; 2.解线性方程; 3.求特征值,特征矩阵; 4.求解行列式4.1 计算逆矩阵
import numpy as np A = np.array([[0,1,2],[1,0,3],[4,-3,8]])print("A = ")print(A)inverse = np.linalg.inv(A)print("A的逆矩阵:")print(inverse)I = A * inverseprint("when A and inverse is ndarray object,\n" "A * inverse =")print(I)I = np.matrix(A) * np.matrix(inverse)print("when A and inverse is matrix object,\n" "A * inverse =")print(I) 上面一段代码的运行结果如下:
A =
[[ 0 1 2] [ 1 0 3] [ 4 -3 8]] A的逆矩阵: [[-4.5 7. -1.5] [-2. 4. -1. ] [ 1.5 -2. 0.5]] when A and inverse is ndarray object, A * inverse = [[-0. 7. -3.] [-2. 0. -3.] [ 6. 6. 4.]] when A and inverse is matrix object, A * inverse = [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
4.2 解线性方程组
使用numpy.linalg.solve函数计算线程方程组,需求如下:已知线性方程组,求解x,y,z
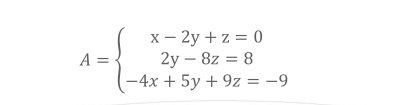
线性方程组.png
import numpy as npA = np.mat("1 -2 1;0 2 -8;-4 5 9")print("A =")print(A)B = np.array([0,8,-9])print("B =")print(B)Solve = np.linalg.solve(A,B)print("Solve:")print("x = {0}, y = {1}, z = {2}".format(*Solve)) 如果A为numpy.ndarray对象,代码运行结果一样。
上面一段代码的运行结果如下:A =
[[ 1 -2 1] [ 0 2 -8] [-4 5 9]] B = [ 0 8 -9] Solve: x = 29.0, y = 16.0, z = 3.0
4.3 特征值和特征向量
特征值是方程Ax = ax的解,是一个标量。其中A是一个二维矩阵,x是一个一维向量。
特征向量是关于特征值的向量。 在eigvals函数可以计算矩阵的特征值,而eig函数可以返回一个包含特征值和对应的特征向量的元组。import numpy as npA = np.mat("3 -2;1 0")print("A =")print(A)print("A矩阵的特征值:")print(np.linalg.eigvals(A))print("A矩阵的特征向量:")print(np.linalg.eig(A)[1]) 上面一段代码的运行结果如下:
A =
[[ 3 -2] [ 1 0]] A矩阵的特征值: [2. 1.] A矩阵的特征向量: [[0.89442719 0.70710678] [0.4472136 0.70710678]]
6.3金融函数
1.fv函数:计算所谓的终值,即基于一些假设给出的某个金融资产在未来某一时间点的价值。
`
转载地址:http://cwiyl.baihongyu.com/
你可能感兴趣的文章
自定义动态生成折线图
查看>>
使Linux支持NTFS分区
查看>>
汇聚各种android开源项目源码分类总汇-IT蓝豹
查看>>
mysql互主自动化配置脚本
查看>>
nginx的upstream模块
查看>>
Plycom CX话机版本升级
查看>>
RHCS+Conga+GFS+cLVM共享存储的高可用性web集群
查看>>
Vmware vsphere 5.5之网络配置
查看>>
设置SVN,Git忽略MAC的.DS_Store文件的方法
查看>>
电信光纤接入的交换机怎样与无线路由器连接设置
查看>>
用Spring4.04来管理Servlet
查看>>
centos6 配置外发邮件
查看>>
OGC和Khronos建立合作关系,共同推动地理信息和3D图形社群的交互操作
查看>>
代码大全的总结
查看>>
欢迎来到JIT的世界: The Joy of Simple JITs
查看>>
android init 启动过程分析
查看>>
学习使用码云上传和下载代码并创建分期
查看>>
Sphinx2.2.11在windows7 下的安装使用
查看>>
AVFoundation 初解
查看>>
独立undo表空间在线回收
查看>>